Ley de Gauss (electromagnetismo)

La ley de Gauss permite el cálculo del campo eléctrico para superficies con alta simetría y nos dice:

 

¿Qué representa esta expresión?, nos dice que la integral en una superficie cerrada del campo por una superficie es igual a la carga interior partida por la constante dieléctrica.

Vamos a intentar aclarar qué quiere decir esto. El miembro de la izquierda representa el flujo de campo eléctrico, que no es más que la cantidad de campo eléctrico que pasa por unidad de superficie.

En esta explicación de la ley de Gauss no hemos hecho referencia a todo el formalismo matemático, ya que esta ley proviene de un teorema matemático mucho más general (teorema de la divergencia).

El siguiente concepto que es necesario introducir es el concepto de densidad de carga. Para entender su significado pensemos en la densidad de un cuerpo, que se define como la masa por unidad de volumen. Pues bien, en densidad de carga eléctrica podemos encontrar densidad lineal, superficial y volúmica de carga. Esto quiere decir que las cargas eléctricas están distribuidas en una recta, en una superficie y en un volumen.

Vamos a ver un ejemplo de aplicación de la ley de Gauss. Supongamos que tenemos una carga eléctrica y queremos calcular el campo eléctrico que genera esta carga en todo el espacio. Aunque ya conocemos la respuesta por la misma fórmula del campo eléctrico, usaremos la ley de Gauss.

Si analizamos la ley de Gauss, el miembro de la izquierda representa la superficie gaussiana sobre la que calcularemos el campo. Esta superficie la ponemos nosotros y tiene que ser simétrica para que el campo tenga el mismo valor en cada punto de esta superficie.

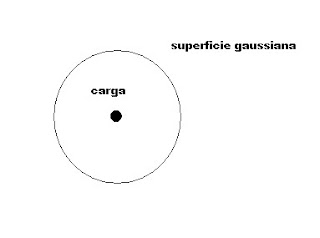
En el caso de una carga puntual, la superficie gaussiana a escoger será una esfera, ya que en todos los puntos de su superficie el valor del campo será el mismo. 

En la figura podemos ver la superficie gaussiana que envuelve a la carga puntual.
Pero ahora, ¿cómo vamos a calcular el campo eléctrico? En primer lugar es importante recordar que el campo eléctrico es un vector y por tanto tiene una dirección. El diferencial de superficie de la fórmula también es un vector. ¿Qué pasa si los vectores son perpendiculares?, que su producto escalar es cero. Es por ello, que es condición indispensable que los vectores E y dS sean paralelos. Recordar que las lineas de campo eléctrico salen de las cargas negativas y van a las positivas, èro en este caso nos es igual el signo de la carga, ya que lo único que nos interesa es su dirección ya que debe ser paralela al dS. ¿Qué pasa con dS? Pues bien, sin entrar en disquisiciones matemáticas, asumiremos que el dS siempre es perpendicular a la superficie que representa.

Como vemos en la imagen el vector de campo eléctrico sale de la carga y es paralelo al vector dS. Pero ahora queda resolver la integral, que como veremos es muy fácil. El por qué es bien simple, si nuestra integral es sobre una curva cerrada para un dS, ¿qué pasa si integramos el dS sobre toda la superficie?, pues que lo que obtenemos es la expresión de la superfície para la geometría que tenemos. En palabras más sencillas, la integral sobre toda la superfície no es más que la fórmula de la superficie de una esfera.

Después de todo esto, ¿como nos queda la expresión para este caso dado?

Como vemos, la expresión inicial se ha simplificado mucho, resultando una ecuación con variables conocidas, que son:
E: campo eléctrico
S:superfície de la esfera, que corresponde a la superfície gaussiana elegida, siendo r, el punto donde queremos calcular el campo eléctrico.
La ley de Gauss para este caso queda pues:




Que es de sobras conocida, ya que es el campo E creado por una carga puntual en cualquier punto del espacio.
Sólo queda explicar cual es el significado de Qint. Representa la carga interior a la superficie gaussiana. Esto quiere decir que si no hay carga dentro de la superficie gaussiana, el campo E es 0. Consejo: dibujad todas las superficies gaussianas posibles que contengan y no la carga o conductor para encontrar el campo en todos los puntos del espacio.
En próximas entradas de nuestro blog, se profundizará tanto en el formalismo matemático que conlleva la ley de Gauss, así como ejemplos más complejos de aplicación de esta misma ley.