Microeconomía
Elasticidad (I)
Hola a todos,
Con esta entrada inauguramos una nueva temática a nuestro blog: la microeconomía. Como sabéis, la microeconomía es aquella rama de la economía que se centra en las pequeñas unidades de decisión, como son las empresa, hogares, individuos.....
Dentro de la microeconomía se tratan matemáticamente diversos conceptos, pero en esta entrada introducimos el concepto de elasticidad. El concepto de
elasticidad mide la amplitud de la variación de una variable cuando varía otra
variable de la que depende. Este concepto se aplica a las curvas de demanda y
de oferta para medir la variación de la cantidad demandada u ofertada a raíz de
variaciones de las variables que las determinan.
Existen
diferentes tipos de elasticidad, según se aplique a la oferta o a la demanda,
de manera que se pueden definir 4 tipos de elasticidad:
Todos los tipos de elasticidad se basan en la variación de una variable respecto a otra, de manera que matemáticamente, la elasticidad se calcula como una derivada.
Veamos como se calcula cada tipo de elasticidad, para posteriormente introducir algunos ejemplos.
1. Elasticidad de demanda
Es aquella elasticidad que proporciona información sobre la variación de la demanda ante los cambio en el precio de un bien y viene determinada por la expresión:
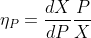
La elasticidad de demanda también informa de cómo reacciona el gasto de los consumidores al variar el precio del bien.
Según el valor de la elasticidad de la demanda tenemos:
1. Si la elasticidad es mayor que 1 (puntos elásticos), el cambio en la cantidad demandada es mayor que en el precio.
2. Si la elasticidad es igual a 1 (elasticidad unitaria), el cambio en la demanda es igual al cambio en el precio.
3. Si la elasticidad es menor que 1 (puntos inelásticos), el cambio en la demanda es menor que en el precio.
4. Si la elasticidad es igual a 0 (demanda perfectamente inelástica o rígida), la demanda no cambia con la variación en el precio.
5. Si la elasticidad vale infinito (demanda perfectamente elástica), la demanda varía sin necesidad de que lo haga el precio.
Una vez vistos los diferentes casos según el valor de la elasticidad de demanda, es necesario ver, cuáles son los factores que la determinan. Éstos son:
- Tipo de bien
- Posibilidad de sustitución del bien
- Como influye el tiempo en la respuesta a las variaciones de precio
Ejemplo 1:
Sea la función de demanda
X=-1000*P+4000
¿Cuál es el valor de la elasticidad para un bien de precio P=2?
En primer lugar, recordar la definición de la elasticidad de demanda:
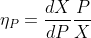
después se calcula dX/dP= -1000
y para conocer el valor de X en el punto P, sólo es necesario sustituir el valor de P del enunciado en la expresión de la demanda. En este caso X=2000.
Ahora, se sustituyen los valores en la expresión de la elasticidad:
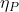
=-1000*(2/2000)=-1
Ejemplo 2:
Un consumidor tiene una función de demanda X+3P=24, ¿qué gasto realiza en el punto de la demanda que tiene una elasticidad de 5?
De la expresión de la demanda, se despeja la X, de manera que X=24-3P
Aplicando la definición de elasticidad de la demanda, se tiene que:
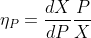
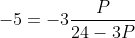
De esta ecuación se despeja el valor de P. En este caso P=6,66
Mientras que sustituyendo en la expresión de la demanda se obtiene que X=4.
Sabiendo que el gasto es el producto de X.P, ya que corresponde a cantidad de demanda por su precio, el gasto es:
Gasto=X.P=4.6,66=26,66
En la próxima entrada se tratarán el resto de elasticidades con ejemplos para cada una de ellas.
Esperamos que os haya sido de utilidad y si es así, os podéis suscribir a nuestro
blog,
canal de Youtube o visitad nuestra
web!